다이나믹프로그래밍 백준 1932 문제 풀입니다.
▶ 문제
우선 dp[i][j] 의 형태로 점화식이 만들어 질 것 같네요. 그렇게 생각을 한 이유는 아래층에 있는 수(1) 는, 현재 층에서 선택된 수의 왼쪽대각선 또는 오른쪽 대각선 (N) 에 있는 것 중에서만 선택을 할 수 있다고 하였으니까요.
1개의 숫자가 선택을 할 수 있는 경우의 수는 2가지이네요. 그렇기 때문에 dp[i][j]의 형태의 점화식이 만들어 질 것입니다.
자, 문제 해결의 키포인트 입니다. 각 숫자의 맨 왼쪽과 오른쪽은 항상 일정한 위치의 값만 받아올 수 있습니다.
위의 그림을 예로 들면 3이 선택할 수 있는 숫자는 오른쪽에 있는 7과 왼쪽에 있는 어떠한 값이겠네요. 그런데 왼쪽에는 값이 없죠. 그렇기 때문에 맨 왼쪽에 있는 숫자는 항상 바로위에 있는 값만 받아올 수 있는 것이죠.
그렇기에
if ( j == 1)
dp [i][j] = dp[i][j] + dp[i-1][j] 가 되겠네요.
맨 오른쪽에 있는 경우는 한번 생각을 해보시길 바랍니다.
점화식은
if ( j==i)
dp [i][j] = dp[i][j] + dp[i-1][j] 가 됩니다.
이해가 잘 안된다면 아래의 그림을 보면서 천천히 이해를 해보시길 바래요.
그렇다면 중간에 있는 값은 어떠한 식이 세워질까요? 이건 뭐 특별한 경우가 없죠. 왼쪽 대각선과, 오른쪽 대각선에서 내려받는 값 중 큰 값을 선택하면 됩니다.
점화식으로 표현을 하면
dp[i][j] = dp[i][j] + MAX ( dp[i-1][j] , dp[i-1][j-1] )이 됩니다.
정리를 해보면 점화식들의 표현은
1 2 3 4 5 6 | if(i==1) { dp[i][j] = dp[i][j] + dp[i-1][j]; } else if (i==j) { dp[i][j] = dp[i][j] + dp[i-1][j-1]; } else dp[i][j] = dp[i][j] + Math.max(dp[i-1][j], dp[i-1][j-1]); | cs |
이렇게 나타나게 됩니다.
완성된 코드를 보도록 하겠습니다.
[ JAVA ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); // 삼각형의 크기 int dp[][] = new int[n+1][n+1]; int max = 0; for(int i=1; i<=n; i++) { for(int j=1; j<=i; j++) { dp[i][j] = sc.nextInt(); if(i==1) { dp[i][j] = dp[i][j] + dp[i-1][j]; } else if (i==j) { dp[i][j] = dp[i][j] + dp[i-1][j-1]; } else dp[i][j] = dp[i][j] + Math.max(dp[i-1][j], dp[i-1][j-1]); if(max < dp[i][j]) max = dp[i][j]; } } System.out.println("최대값 :" + max); } | cs |
아직 저도 초보이지만 쪼개는 방법의 패턴은 생각보다 그리 많지가 않아서 반복적으로 많이 풀다보면 생각보다 점화식이 떠오르는 경우가 많이 있습니다. 틀리더라도 점점 비슷해져가는 모양을 보실 수 있으니 기죽지 말고 많이 풀어보시길 바랍니다!










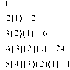

최근댓글